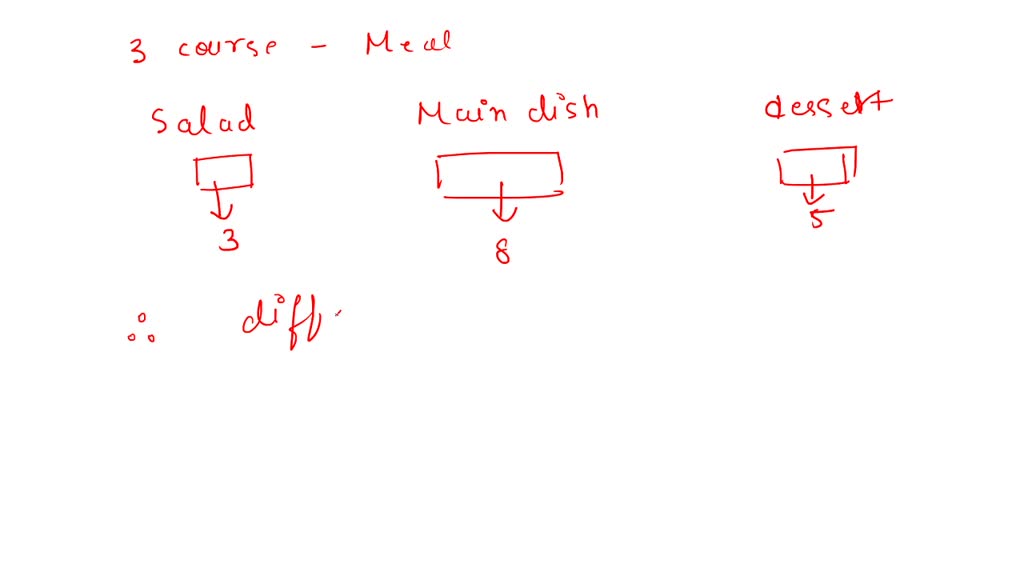
vaultanna.blogg.se - Math counting principle

#Math counting principle series

But we have overcounted here, since subsets are unordered. There are 6 children and 6 benches for them to sit. We choose any of $n$ elements at first, then any of the $n-1$ elements left, and continue, for $$n \cdot (n-1) \cdots (n- k +1)$$ choices. As a first attempt, we could count them by picking $k$ elements in order. The usual example is counting the number of subsets of size $k$ from $n$ elements. Now that you have a basic understanding, move on to the Got It? section to check your skills.To count the number of cows in your field, first count the number of legs and then divide by four. Think about how many different outfits you have:ģ pants * 6 shirts * 2 shoes = 3*6*2 = 36 possible outfits You are going through your suitcase to see how many outfits were packed, and find three pairs of pants, six shirts, and two sets of shoes, since we were packing very light.įor now, don't worry about matching.This gives us the same result with much less work and drawing! Using the Fundamental Counting Principle, we can rewrite the number of options for each type of food as a product to find the total number of combinations:ģ(sandwiches) * 3(sides) * 2(drinks) = 18 possible combinations Instead of drawing out the 18 different possibilities in a tree diagram, we can use the idea of the Fundamental Counting Principle to solve for the number of possible combinations. The Fundamental Counting Principle states that if one event has m possible outcomes and a second independent event has n possible outcomes, then there are. Solution: There are 18 total combinations. Sandwiches: Chicken Salad, Turkey, Grilled Cheeseĭraw a tree diagram to find the total number of possible outcomes.With the combo meal, you get 1 sandwich, 1 side, and 1 drink. Look at the tree diagram for this problem:Ī new restaurant has opened, and they offer lunch combos for $5.00. Learn about the Fundamental Counting Principle also known as the multiplication counting principle in this video by Mario's Math Tutoring. However, this can be applied to an infinite number of choices or possibilities, which opens the door for some neat shortcuts.

If there are m ways to choose a first item, and n ways to choose a second item, after the first item has been chosen, then there are m*n ways to choose both items.

The idea of combinations and permutations offers an opportunity to skip the tree diagram and still get the correct answer without spending hours drawing lines and making sure you haven't skipped an outcome.īefore we can discuss combinations and permutations, we must first understand the idea of the Fundamental Counting Principle (FCP), that states: However, there are usually way too many possibilities, making a tree diagram impractical. The concept of sum and product rule has also been explained with help of examples. Sometimes, when we are talking about the idea of probability, it is possible to create a tree diagram that has all possible outcomes. 1.3K 78K views 1 year ago Discrete Structures The basic counting principles has been explained in this video.

#Math counting principle series

So far in this Probability: An Overview series of Related Lessons, found in the right-hand sidebar, you have studied experimental and theoretical probability as well as dependency.